INTEGRACION POR PARTES
El Acrónimo ILATE para la Selección de Funciones
El acrónimo ILATE es una guía para elegir la función u en la integración por partes, ordenando las funciones por prioridad: Logarítmica, Inversa trigonométrica, Algebraica, Trigonométrica y Exponencial. Se selecciona como u la función que aparece primero en esta jerarquía dentro del integrando. Por ejemplo, si el integrando incluye una función logarítmica y una exponencial, la función logarítmica se elige como u y la exponencial como parte de dv, facilitando así la integración. y
y  . Entonces su derivada está dada por
. Entonces su derivada está dada por
Si integramos ambos lados de la ecuación, obtenemos

Luego, si pasamos  al lado izquierdo, obtenemos
al lado izquierdo, obtenemos

1Elegimos  y calculamos
y calculamos  y
y 
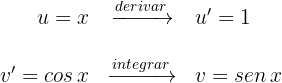
2Sustituimos los valores de  y
y  en la fórmula de integración por partes
en la fórmula de integración por partes
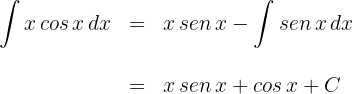

Tenemos el producto .
Observad que no importa si es ó , ya que obtenemos un seno tanto si derivamos como si integramos. Sin embargo, ya sabemos que es mejor considerar para reducir su grado.
Derivamos para calcular :
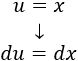
Integramos para calcular :
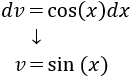
Aplicamos la fórmula de integración por partes:
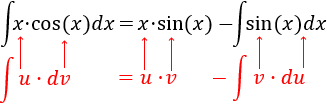
Solo queda calcular la integral de , que es , y añadir la constante de integración :
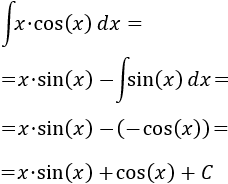
Recuerden que aquí abajo les dejare los links por si ustedes quieren indagar un poco más , muchas gracias y suerteeeee :) .
https://www.matesfacil.com/resueltos-integracion-por-partes.htmhttps://www.superprof.es/apuntes/escolar/matematicas/calculo/integrales/integracion-por-partes-i.html
https://cards.algoreducation.com/es/content/TmGSy1PT/integracion-por-partes
Comentarios
Publicar un comentario