LIMITES
"Cuando los valores atribuidos sucesivamente a una variable se aproximan indefinidamente a un valor fijo para llegar por último a diferir de ese valor en una cantidad tan pequeña como se desee, entonces dicho valor fijo recibe el nombre de límite de todos los demás valores."
Propiedades de los límites
Algunas propiedades matemáticas de los límites pueden facilitar en algunos casos los cálculos en funciones más complejas. Considerando dos funciones definidas en un mismo intervalo.
- Unicidad del límite: El límite de una función será único en caso de su existencia.
- Límite de una constante: El límite de una función constante 𝑓(𝑥) = 𝚔 será igual a la constante 𝚔.
- Suma y resta de límites: El límite de la suma será la suma de los límites.
- Producto de límites: El límite del producto de una constante por una función será la constante por el límite de la función.
Ver más propiedades en la versión extendida
Ejemplo
Calcular el límite de 𝑔(𝑥) · 𝑓(𝑥) cuando 𝘹 tiende a 1 para 𝑔(𝑥) = 𝘹 - 1 y 𝑓(𝑥) = 𝘹 + 1
Usando las propiedades antes definidas tenemos:
Límites que tienden al infinito
¿Cómo conocemos el límite de una funcíón cuando sus variables tienden a infinito?
En este caso la manera de resolverlo resulta complicado, debido a que al evaluar una función en infinito el resultado es una función indefinida. A pesar de eso, es posible conocer el valor del límite de la función cuando los valores tienden a infinito.
Ejemplos de límites
Encontrar los siguientes límites:
- 𝑓(𝑥) = 𝘹2 cuando 𝘹 tiende a 4.
- 𝘹2 + 8𝘹 + 31 cuando 𝘹 tiende a 3.
- 𝘹2 - 𝘹 + 2 cuando 𝘹 tiende a 2.
Límite 1 
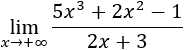
Tenemos la indeterminación infinito partido infinito.
La función es un cociente de polinomios de distinto grado. Como el grado del polinomio del numerador es mayor que el del denominador, el límite es infinito:
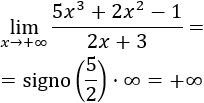
El infinito es positivo porque el cociente de los coeficientes principales de los polinomios es positivo.
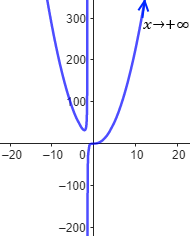
Gráfica de la función:
Nota: si el coeficiente del polinomio del denominador fuese negativo, entonces el resultado del límite también lo sería:
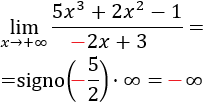
Límite 2 
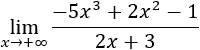
La función es como la del límite anterior, pero ahora el coeficiente director del numerador es negativo.
Razonamos como en el límite anterior:
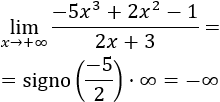
En este límite, el infinito del resultado es negativo porque el coeficiente principal del polinomio es negativo.
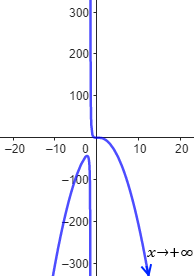
Gráfica de la función:
Nota: si el coeficiente del polinomio del denominador fuese negativo, entonces el resultado del límite sería positivo:
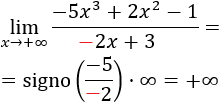

RECUERDEN QUE AQUI ABAJO DEJARE LOS LINKS POR SI USTEDES GUSTAN INDAGAR MAS , MUCHAS GRACIAS..
https://www.matesfacil.com/BAC/limites/ejercicios-resueltos-limites-1.html
Comentarios
Publicar un comentario